通过trace,追踪数据流与数据运算,还原被VMP保护的算法
主要技术点有两个:
unidbg模拟执行结果和真机不一致,需要排查暗桩
该签名有一个VMPsha256算法,我们需要通过trace,还原出VMPsha256的入参,才能继续向上分析
1. 分析
{
"b1":"6bbc8976-d0fe-44ef-9776-ab9da0c127e8",
"b2":"3.2.8.4_0_0",
"b3":"2.1",
"b4":"JwAYqqazvFPldvFSbFjzS8Y5YPF/nzW8K524+TNQmdxhnuDQqUQTDNSFPDfqkulYd8Q69F7zTWcfhrWWUPVE4yv9LFGN3bfUSxOuFKt02/3c1QITOTMBCf/2FeJLYLP4ghsxnB2jTZYjbhoEC4NAZztvBaJ9E4uAvBSzMHnMSwjgzF1my9BgY/3eIYU2HlO2NVU7FCsKYGCeHyZ2ch462MraGQenp69pS+BNrObt2kin/tGXmx02PLFAIk0AT5xVBfWsVshy43w3hUXsyrK43xYL0UzvadWRqSdm17LVgfh7MIWzF+SkTkkYm4MUY+vOtO8gv+qDB4/lq1Tfi2PJPWNbaPeu9dx/FQ0ANlOugsG079jTNWspdqdA9JbX7mhtv63HGyOmhCNkZ3ck23R19eWNC9e3i3w2UAimyes=",
"b5":"79154e49c97f5d8e36bc36614755281a9b393246",
"b7":"1747484875815",
"b6":"a79660821a3409f39fc9210663b352bcff3f2d0e"
}这里主要以b5为例,展示利用trace还原被VMP保护的算法思路。可以通过tracewrite、memoryscan等方式快速定位到b5计算函数。b5签名部分流程如下:
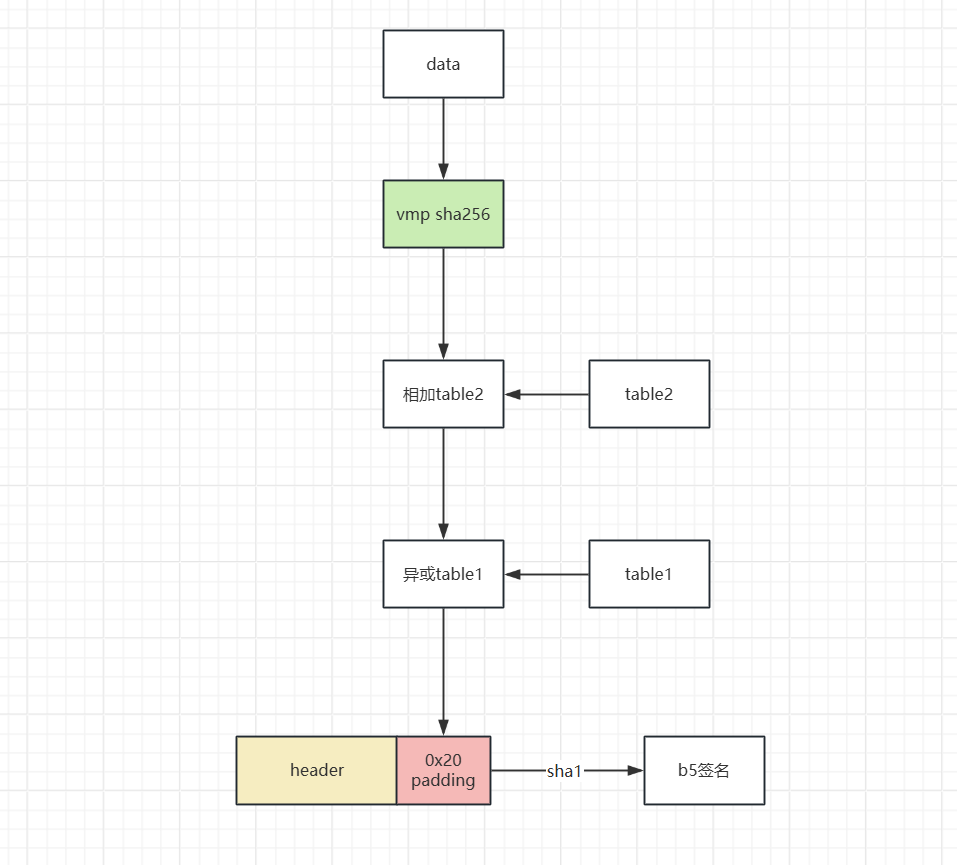
1. 异或table1
b5 入参是请求头+0x20字节数据,然后进行标准sha1计算。接下来我们分析0x20字节数据是怎么生成的。21 97 45 07...
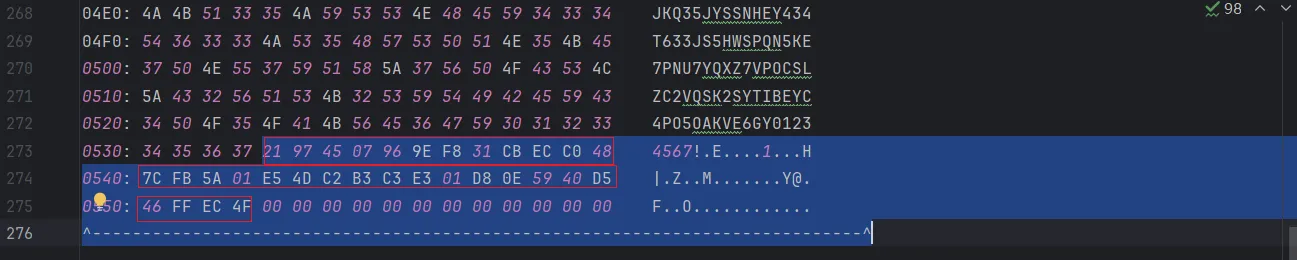
通过tracewrite,定位到数据写入位置0x24674
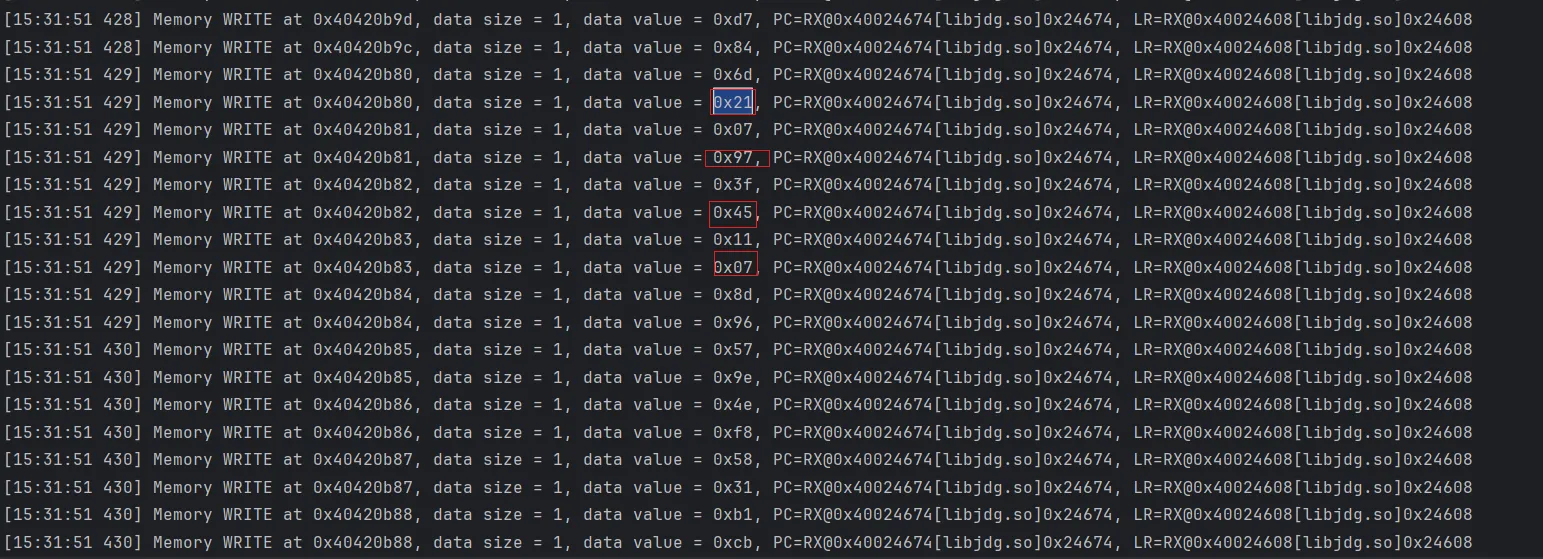
ida 跳转到0x24674,发现位置属于函数sub_24420,通过CFG和函数代码判断,该函数是被VMP保护了

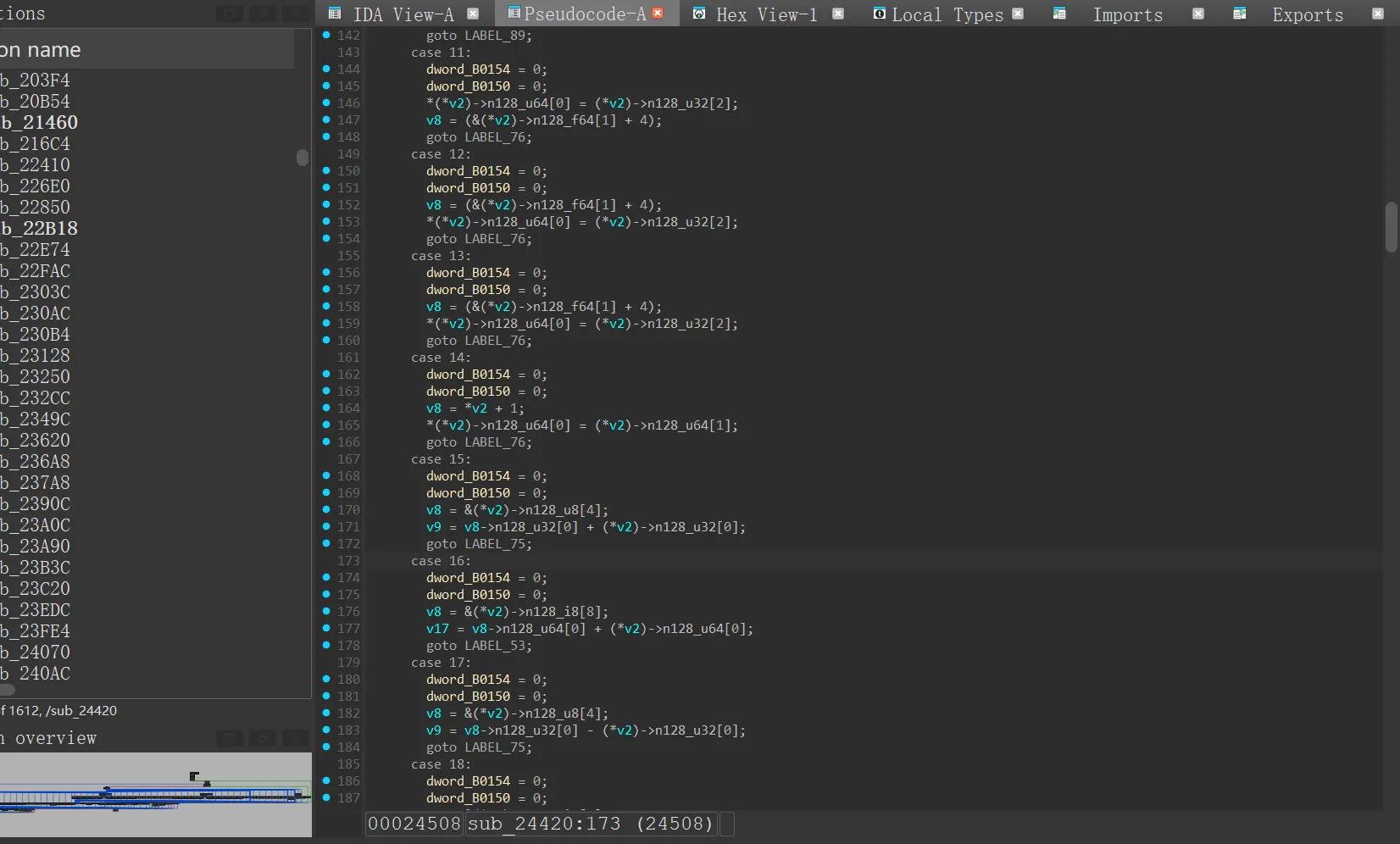
接下来我们要通过unidbg trace还原被VMP保护的签名算法。首先在trace中搜索0x24674 ,定位到21 97 45 07出现位置, 分析代码功能发现,只是赋值,并无计算,不是我们想要的位置。
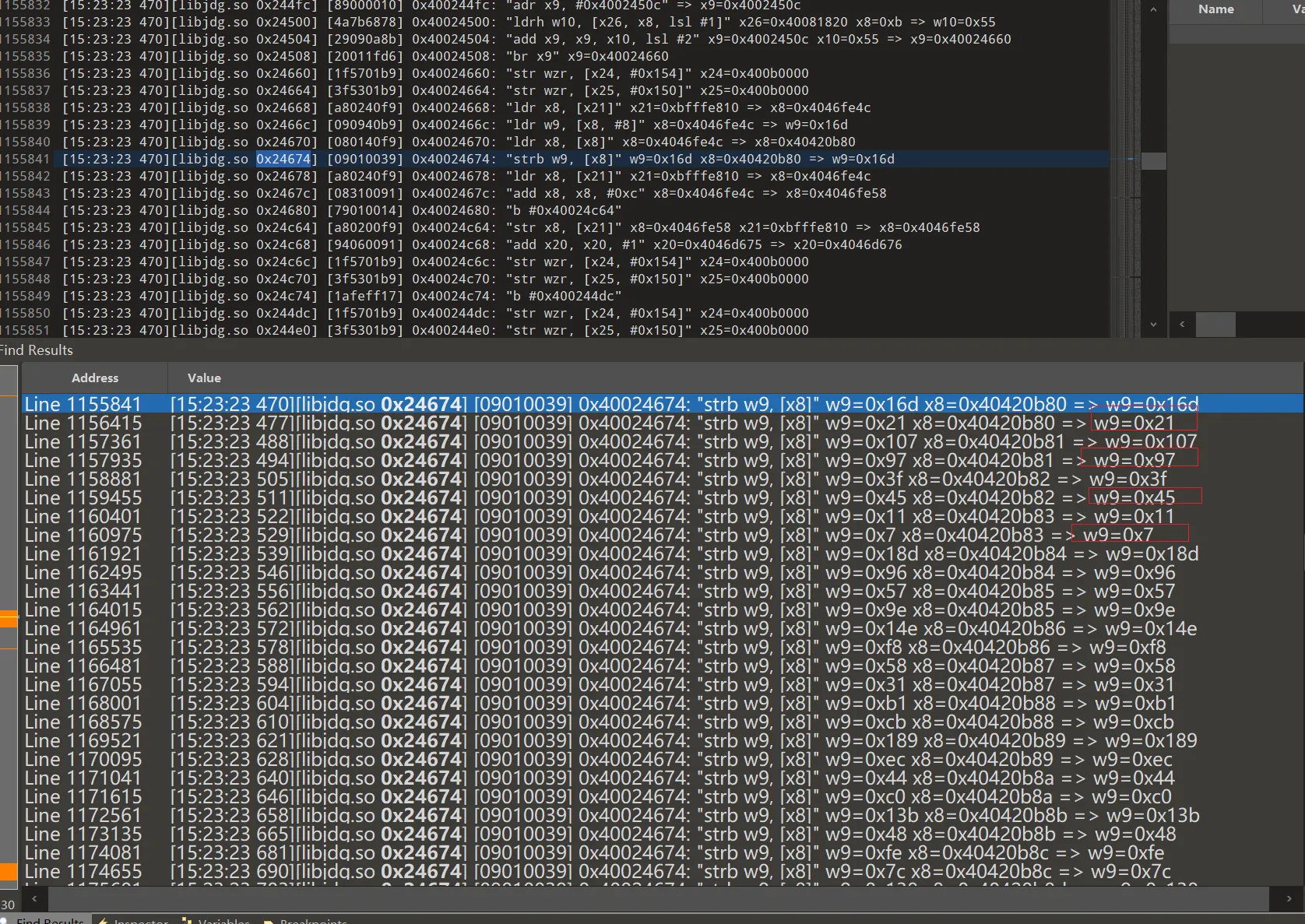
在trace文件中搜索0x21,然后只关注计算出结果的相关指令,最终定位到到0x24918

在trace文件中过滤0x24918,确认定位到计算位置,可以看到主要有两轮,有一个表是固定的表 40 90 7a 16... ,我是通过trace了两次,但是两次参数不同,发现两次trace中有一组表是固定的。
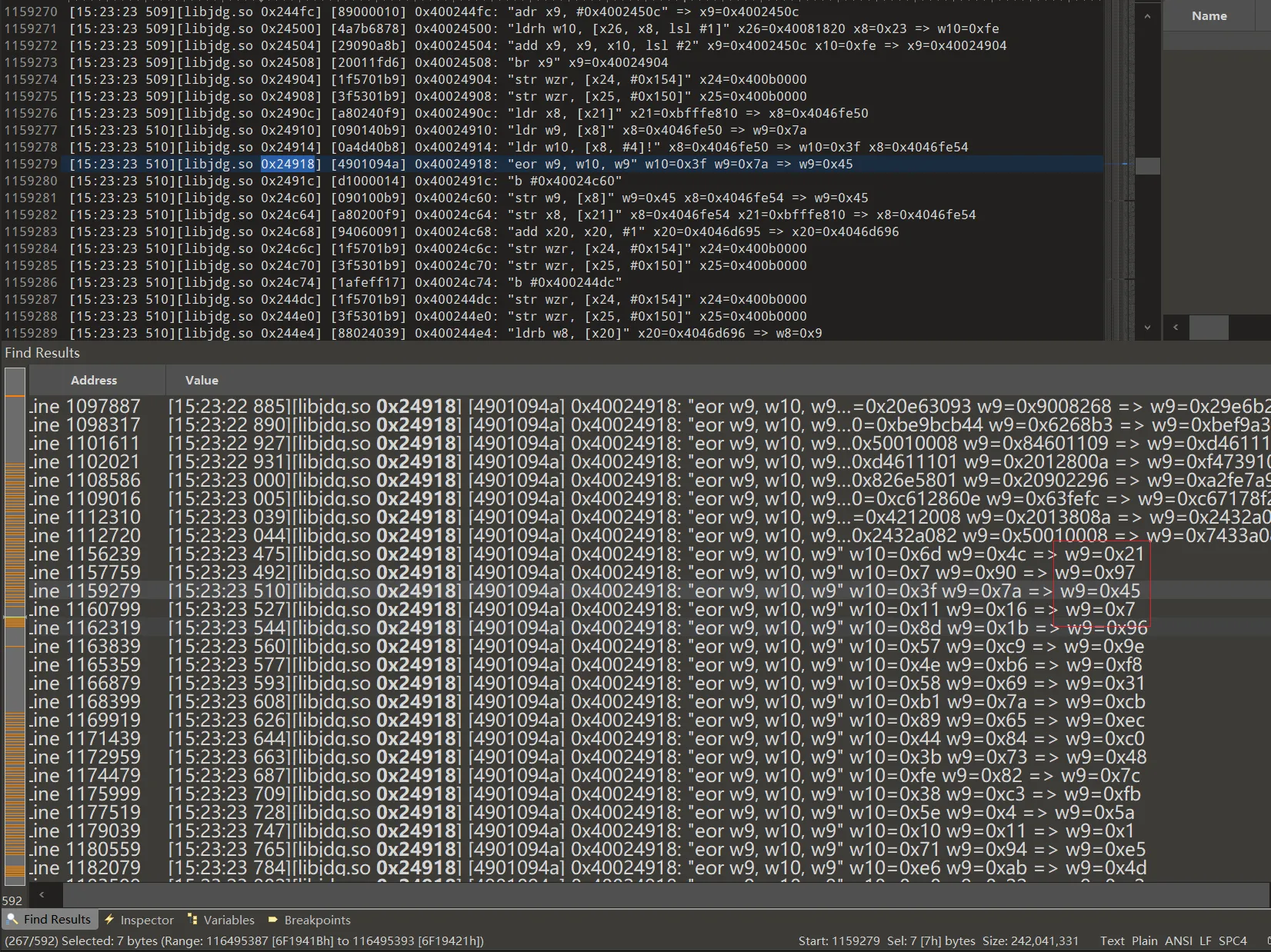
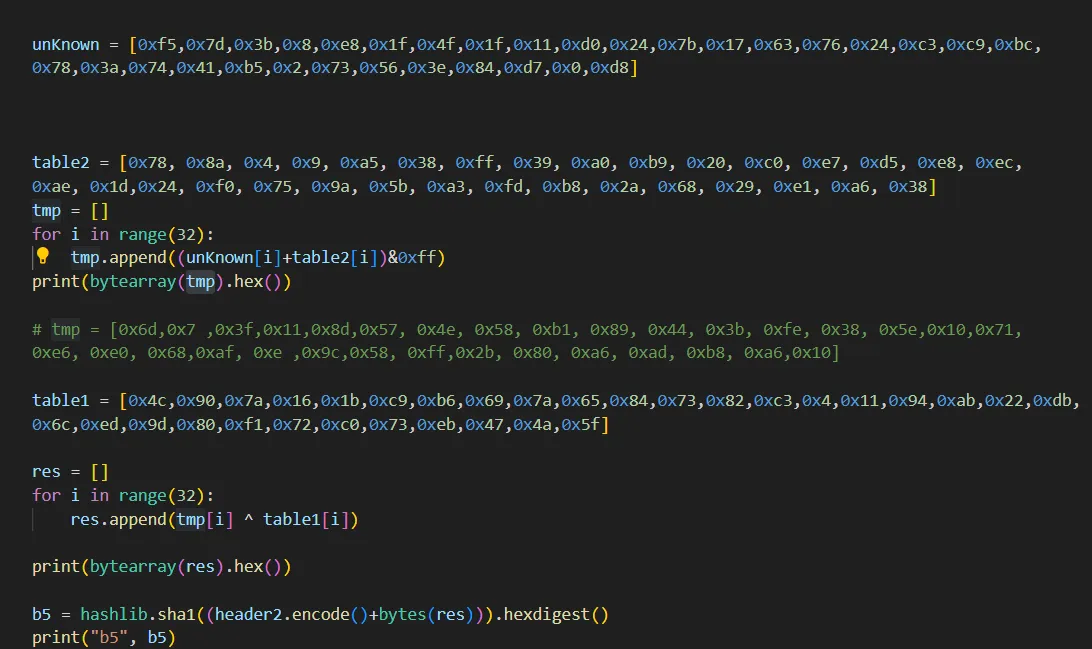
python实现逻辑如下,得到的结果和unidbg主动调用的结果一致。
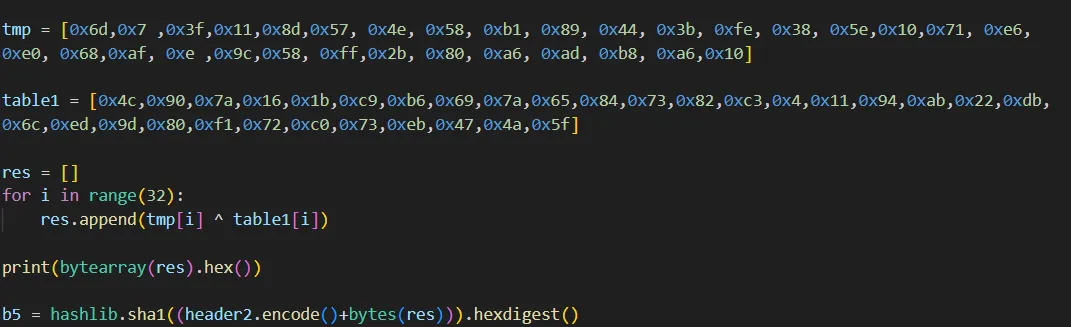

2. 相加table2
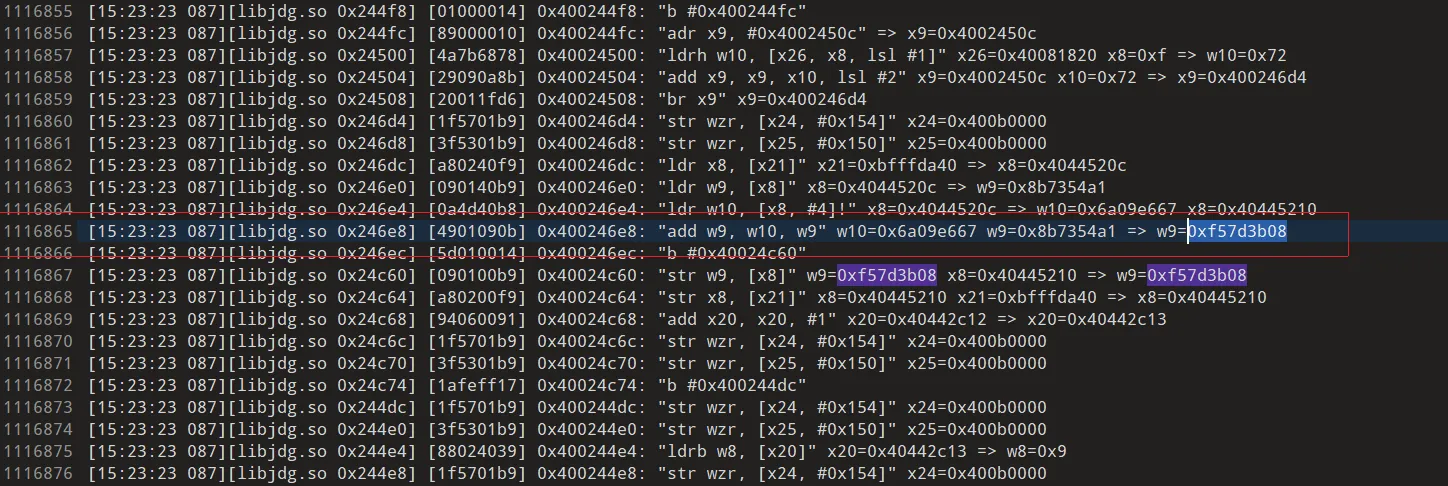
接下来分析tmp 数组中元素是如何生成的,还是通过在trace中搜索,定位到0x246e8处, tmp中来源两个数组中数据相加。
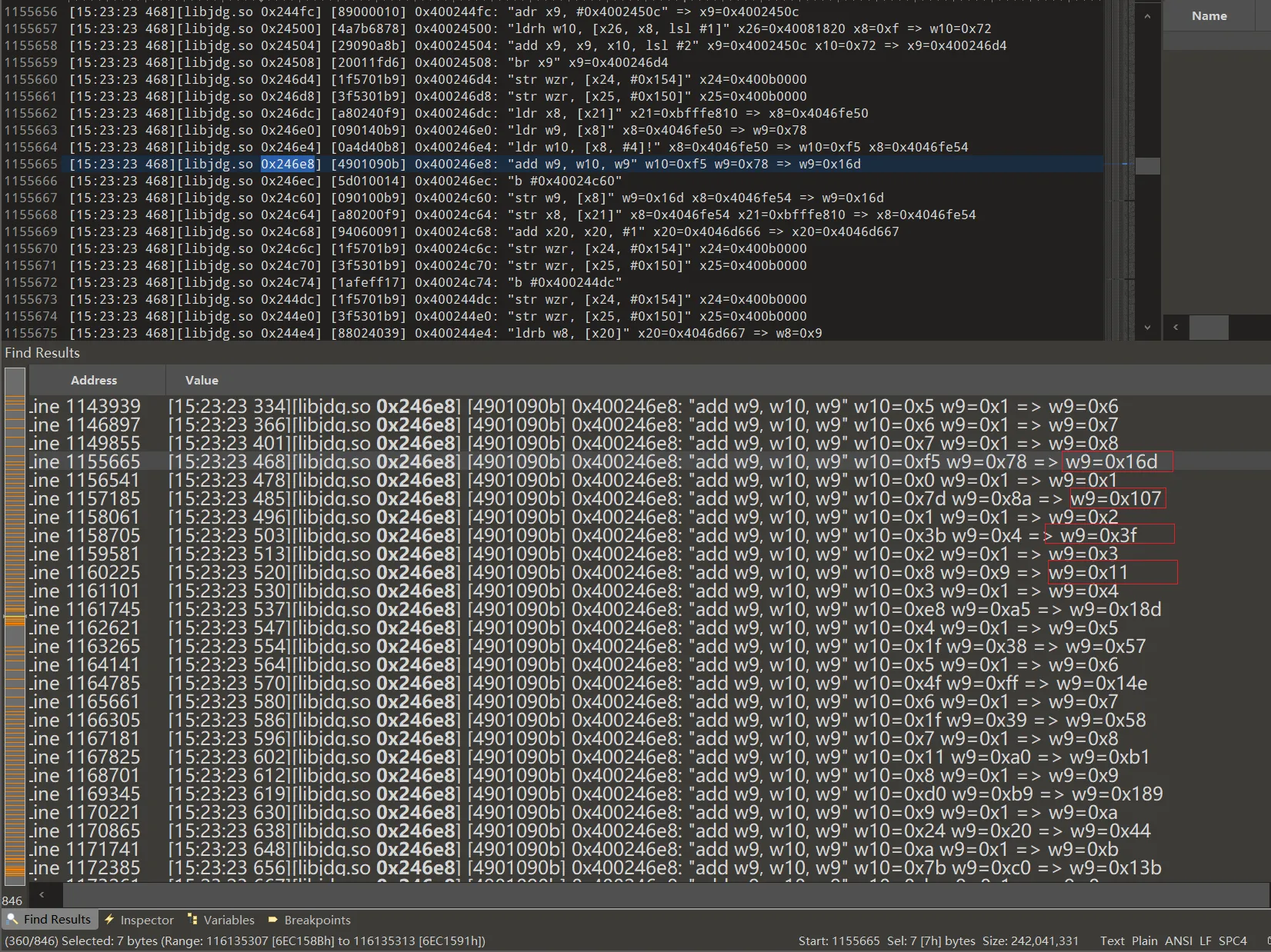
python代码验证如下:

3. vmp sha256
分析 unknown 数据来源 ,搜索 unkown数组前4字节,定位到0x246e8,w10=0x6a09e667 是sha256的初始化iv
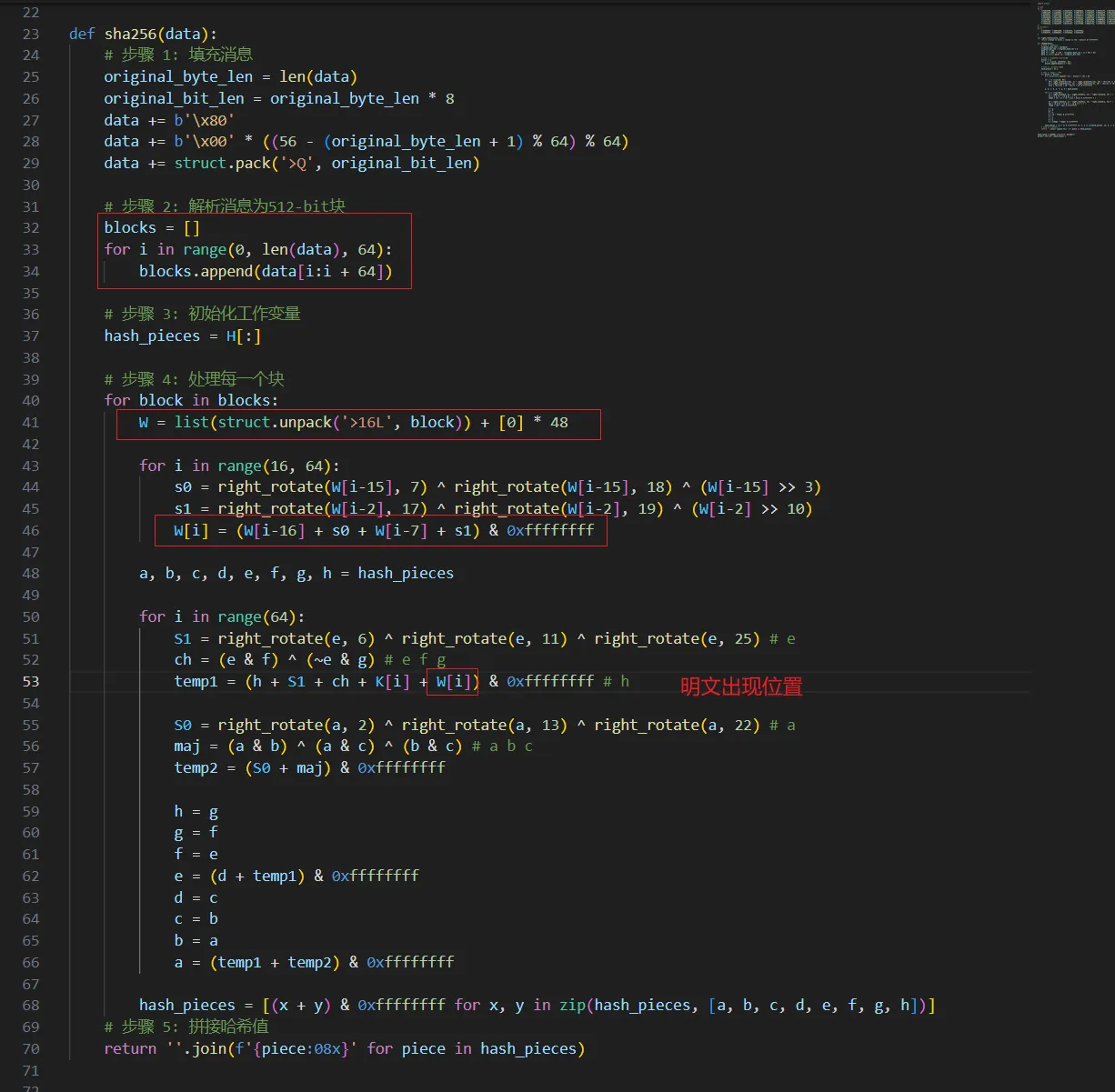
推测是sha256,接着定位输入,对于标准sha256,明文一般出现在以下位置,逆向分析的话,一般分析k表附近。
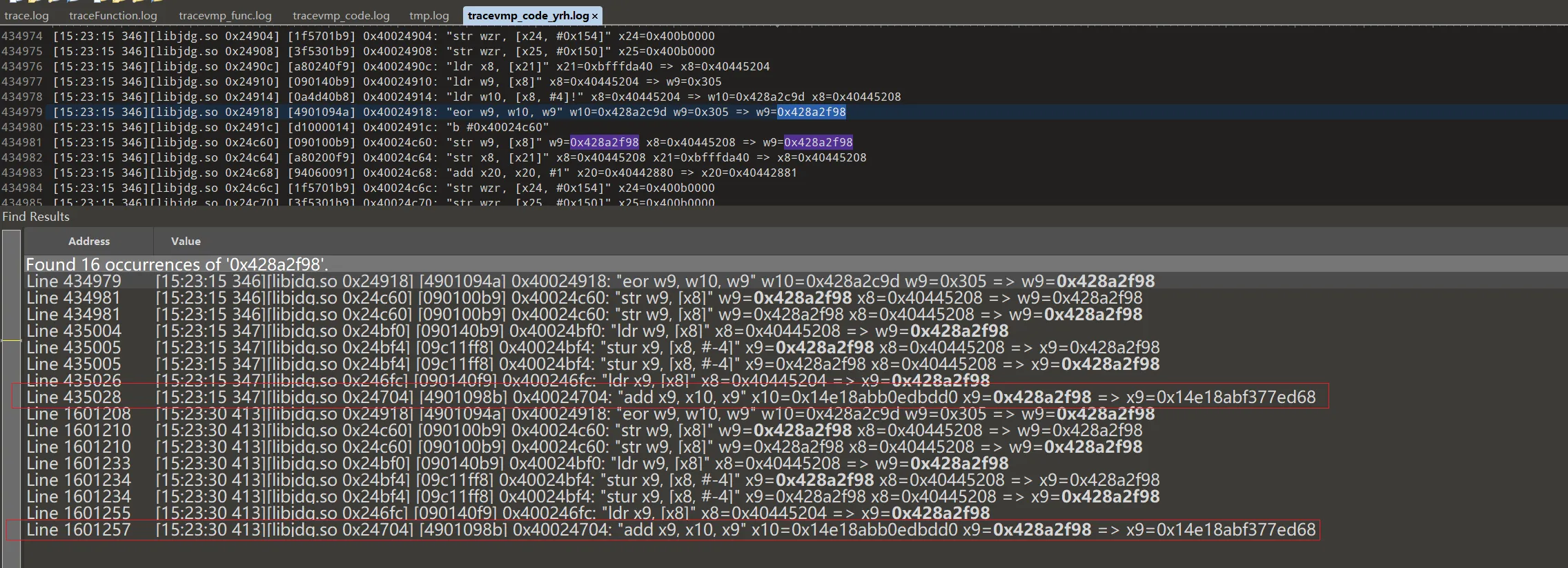
在标准算法中K表是已知的,搜索k表中第一个元素0x428a2f98
分析过程:就是通过trace,一步一步找计算流程,然后识别当中的特征,定位明文
sha256计算步骤
S1 = right_rotate(e, 6) ^ right_rotate(e, 11) ^ right_rotate(e, 25) # e
ch = (e & f) ^ (~e & g) # e f g
temp1 = (h + S1 + ch + K[i] + W[i]) & 0xffffffff # h
trace 搜索 k0 0x428a2f98 定位到:
"add x9, x10, x9" x10=0x14e18abb0edbdd0 x9=0x428a2f98 => x9=0x14e18abf377ed68
x9是 k0
k0 = 0x428a2f98
trace 中搜索 上面与k0相加的 0x14e18abb0edbdd0
"add x9, x10, x9" x10=0x14e18ab9167f444 x9=0x1f85c98c => x9=0x14e18abb0edbdd0
这里不太好判断
继续搜索上面 0x1f85c98c的
"eor w9, w10, w9" w10=0x1104400c w9=0xe818980 => w9=0x1f85c98c
根据sha256计算步骤,异或操作,只有s1计算 或者 ch计算可能进行异或操作
对上面的w10=0x1104400c进行追踪
"and w9, w10, w9" w10=0x510e527f w9=0x9b05688c => w9=0x1104400c
与操作,只有ch计算中包含与操作,所以上面的w9=0x1f85c98c 含义就是ch =0x1f85c98c
也就是说"add x9, x10, x9" x10=0x14e18ab9167f444 x9=0x1f85c98c => x9=0x14e18abb0edbdd0 中
ch = 0x1f85c98c
0x14e18abb0edbdd0 = ch + 0x14e18ab9167f444
trace 中继续搜索 0x14e18ab9167f444
"add x9, x10, x9" x10=0x5be0cd19 x9=0x14e18ab3587272b => x9=0x14e18ab9167f444
0x5be0cd19 在标准sha1中是h
h = 0x5be0cd19
0x14e18ab9167f444 = 0x14e18ab3587272b + h
trace 中继续搜索 0x14e18ab3587272b
"eor x9, x10, x9" x10=0x14e1883b2ae1883 x9=0x2887293fa8 => x9=0x14e18ab3587272b
异或操作,也就是说 s1 = 0x14e18ab3587272b
总结下来就是:
s1 = 0x14e18ab3587272b
0x14e18ab9167f444 = 0x14e18ab3587272b + h
=> 0x14e18ab9167f444 = s1 + h
0x14e18abb0edbdd0 = ch + 0x14e18ab9167f444
==> 0x14e18abb0edbdd0 = ch + s1 + h
0x14e18abf377ed68 = k0 + 0x14e18abb0edbdd0
===> 0x14e18abf377ed68 = h + s1 + ch + k0
trace中搜索 0x14e18abf377ed68, 可以确定0x5c0f60b8 就是w0,也就是明文
"add x9, x10, x9" x10=0x14e18abf377ed68 x9=0x5c0f60b8 => x9=0x14e18ac4f874e20
根据根据规律,搜索k表中元素,之后与k表元素进行add,得到一个tmp,然后搜索与tmp进行add的就是明文了
例如 k[1] = 0x71374491
搜索k1 得到
"add x9, x10, x9" x10=0x3cdc79fe5b6af28 x9=0x71374491 => x9=0x3cdc7a056edf3b9
tmp = 0x3cdc7a056edf3b9
搜索tmp得到
"add x9, x10, x9" x10=0x3cdc7a056edf3b9 x9=0x4e028b63 => x9=0x3cdc7a0a4f07f1c
x9=0x4e028b63就是明文了
如此最终得到明文:
0x5c0f60b8 0x4e028b63 0x30387d0f 0x567eb4c7 0x80000000 0x00000000
可以观察到从第5组开始就是填充了,所以实际明文是:
0x5c0f60b8 0x4e028b63 0x30387d0f 0x567eb4c7
即,这是一个32字节的数据
5c0f60b84e028b6330387d0f567eb4c7如此就通过trace还原了VMP sha256算法,确定了入参vmp sha256,后面再继续通过tracewrite结合trace搜索就可以继续分析了。
2. 补充暗桩排查
通过tracewrite,可以定位到sha1生成b5的函数,然后frida hook真机,发现0x20字节的padding不一样,之后在Unidbg中进行function trace,打印调用函数,在frida 中hook,发现某个函数的返回结果真机和Unidbg模拟的不一致,就定位到了暗桩。
unidbg trace function得到函数调用
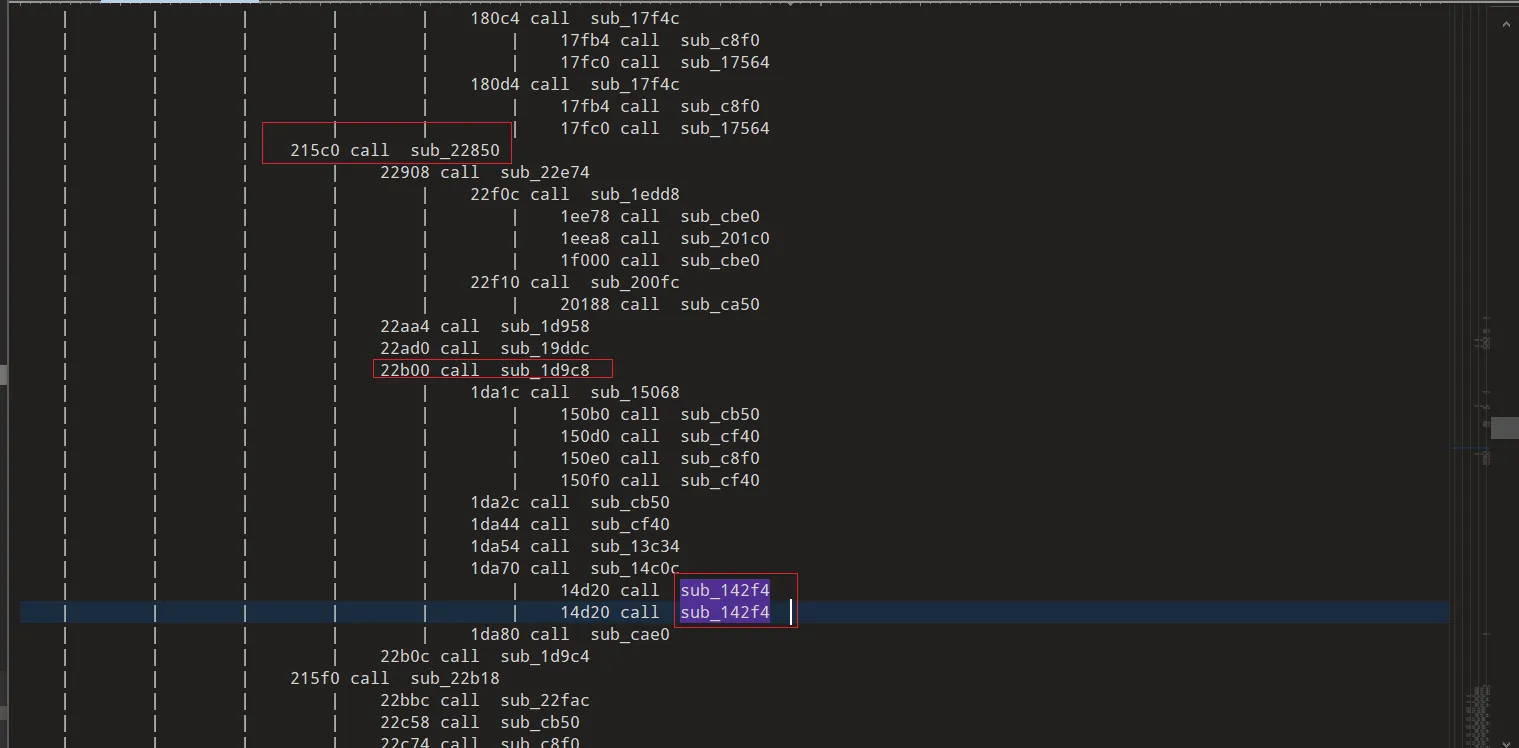
frida hook 之后发现sub_22850会被调用,但是其他的函数都不会被调用了,说明在sub_22850内,模拟器和真机走的分支不同。
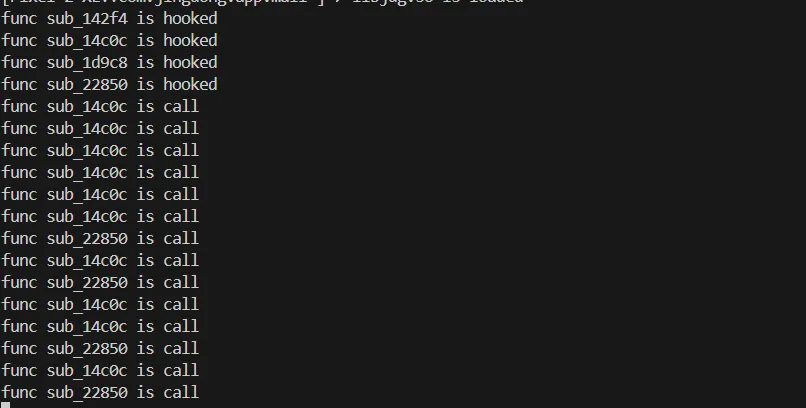
通过hook排查,最终定位到sub_200FC中真机返回0, 模拟器返回1。 patch sub_200FC,让其返回值为0。
public void pathc_sub_200FC(){
emulator.attach().addBreakPoint(module.base + 0x200FC, new BreakPointCallback() {
@Override
public boolean onHit(Emulator<?> emulator, long address) {
RegisterContext context = emulator.getContext();
UnidbgPointer LR = context.getLRPointer();
// 在函数退出时下断,修改返回值x1的值为1
emulator.attach().addBreakPoint(LR.peer, new BreakPointCallback() {
@Override
public boolean onHit(Emulator<?> emulator, long address) {
emulator.getBackend().reg_write(Unicorn.UC_ARM64_REG_X0,0);
return true;
}
});
return true;
}
});
}sub_200FC逻辑如下:可能是真机的随机数生成逻辑与Unidbg模拟器不一致。
bool __fastcall sub_200FC(unsigned int a1)
{
unsigned int v2; // w22
unsigned int v3; // w23
__int64 v4; // x0
dword_B0154 = 0;
dword_B0150 = 0;
v2 = atomic_load(qword_AC8E8);
v3 = atomic_load((qword_AC8E8 + 4));
v4 = random();
dword_B0154 = 0;
dword_B0150 = 0;
return v2 + (v4 % (v3 - v2)) > a1;
}


